Прежде чем мы начнем анализировать квадратичную функцию, было бы полезно вспомнить, что подразумевается под термином «функция» в математике.
Если вы твердо освоите основы о функции (различные методы определения, концепцию графика), последующее изучение различных типов функций будет восприниматься значительно проще.
Что называют квадратичной функцией
Запомните!
Функция, представленная в квадратном виде, является квадратичной функцией.
Если в функции наибольшая степень переменной «x» равна «2», то эта функция является квадратичной. Другими словами, квадратичная функция имеет степень переменной «x» равную двум.
Давайте рассмотрим несколько примеров квадратичных функций и выясним, какие значения имеют коэффициенты «а», «b» и «с».
Как создать диаграмму параболической функции
Запомните!
Параболой называется график квадратичной функции.
Форма параболы представляет собой следующую картину.
Также парабола может быть обратной по направлению.
При построении графика квадратичной функции существует определенный набор инструкций. Мы настоятельно рекомендуем всегда придерживаться этой последовательности действий, чтобы предотвратить возможные ошибки при построении параболы.
Давайте для лучшего понимания этого алгоритма сразу же рассмотрим его на конкретном примере.
Давайте создадим диаграмму для параболической функции « y = x 2 — 7x + 10 ».
Запомните! Если « a >Если символ равен «0», то ветви идут вверх. В случае, если символ равен «a», то ветви идут вниз.
2 + 3x + 2 = 0 », нужно использовать формулу дискриминанта. Она выглядит следующим образом: D = b 2 — 4ac, где a, b и c — это коэффициенты в уравнении. Если дискриминант D > 0, то у уравнения есть два различных вещественных корня. Если D = 0, то у уравнения есть один вещественный корень. А если D < 0, уравнение не имеет вещественных корней. Не забудьте проверить полученные корни, подставив их обратно в уравнение.0Для расчета значения координаты вершины по оси «Ox» необходимо применить соответствующую формулу.
| Отрицательное число -7. |
| 2 · 1 |
Теперь надо выяснить «y0» в уравнение прямой и найти соответствующую координату « y ».»0Чтобы найти значение функции, необходимо обратиться к исходной функции. Возможно, стоит вспомнить, как это сделать, прочитав урок о решении задач на функцию в разделе о поиске значений функций.
Мы заметим координаты вершины параболы, которые равны A (3,5; -2,25). Вершину параболы мы отметим на системе координат. Затем проведем ось симметрии через отмеченную точку, так как парабола является симметричным графиком относительно оси «Oy».
Запомните! Точки пересечения графика функции с осью «Ox» (осью абсцисс) обозначаются нулями функции.
На графике функция и ее нули представлены так: нули функции названы так из-за того, что координата этих точек по оси «Oy» равна нулю. Теперь давайте разберемся, как можно вычислить координаты точек нулей функции до построения ее графика.
Запомните! Для определения координат точек пересечения с осью ординат функции необходимо заменить « y = 0 » на исходную функцию.
Для нахождения корней квадратного уравнения, изначально записанного в виде « y = x 2 — 7x + 10 », мы заменим « y » на « 0 » и решим полученное уравнение относительно переменной « x ».
| 7 плюс корень из 49 минус 4 умножить на 1 и на 10. |
| 2 · 1 |
| 7 ± √ 9 |
| 2 |
| 7 ± 3 |
| 2 |
График квадратичной функции
График квадратичной функции
Для полного понимания смысла следующего текста, необходимо обладать глубокими знаниями о понятии квадратичной функции.
Проверь свои знания, ответь на следующие вопросы:
Если ты мог ответить немедленно, то продолжай чтение.
Если возникли проблемы с пониманием любого из вопросов, рассмотрите еще раз тему «Функция второй степени».
График квадратичной функции — коротко о главном
Определение
Квадратичная функция – функция вида ( y=a >Представим уравнение вида (ax 2+bx+c), где (a) не равно нулю, (b) и (c) – произвольные числа (коэффициенты), (c) – свободный член.
Кривая, которая описывает график квадратичной функции, является параболой.
Увеличение значения параметра a (по модулю) делает параболу более крутой, в то время как уменьшение значения a приводит к расширению параболы.
Максимальная точка кривой параболы
( displaystyle _>Вершина параболы смещается влево тем больше значение коэффициента b.
Подставляем ( displaystyle _>) в функцию ( y=a >При нахождении корней квадратного уравнения ax 2+bx+c=0, мы применяем формулу: x=(-b±√(b 2-4ac))/(2a).
( displaystyle _>=-frac >-4ac>Вершина параболы будет находиться выше, если значение коэффициента b в уравнении параболы будет больше по модулю.
Взаимный элемент (displaystyle c) – это точка, в которой парабола пересекает ось у.
Квадратичная функция и её коэффициенты
Давайте предположим, что вы уже овладели навыком работы с квадратичной функцией. Вам известно, как проанализировать ее график и построить его, исходя из имеющихся точек.
Ну что же, вот она: ( y=a >+bx+c).
Давай вкратце вспомним, в чем заключается функция коэффициентов.
С самого начала нашего пути в построении параболы нам важно определиться с первым шагом. Какую ключевую точку следует учесть при ее создании?
Ты помнишь, как найти координаты этой вершины?
Для нахождения абсциссы используется следующая математическая формула:
Вот так: если увеличивается значение параметра b, то вершина параболы смещается влево.
Ординату вершины можно найти, подставив ( _>Используйте данную функцию для изменения текста и придания ему уникальности.
Попробуй сам и оцени результат. Каковы получились итоги?
Если выполнить все требования и максимально упростить данное выражение, получится:
Итак, если значение ( displaystyle b) увеличивается, то вершина параболы будет располагаться выше.
Давайте, в конечном итоге, займемся созданием диаграммы. Самое простое решение — построить параболу, начиная с точки перегиба.
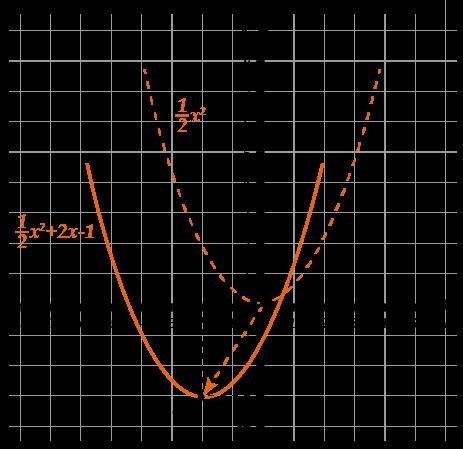
Построить график функции ( y=frac >+2-1).
Решение:
{a}{c} + {b}{d}),( b=frac;text{y} times text{x} times text{z}}{u}), и ( c=frac;text{d} times text{e}}{f}). Затем применяем формулу ( x=frac;text{a} + text{b}}{c}) для вычисления значения x. И наконец, заменяем полученное значение x в формуле ( y=frac;text{a} + text{b}}{c}) для вычисления значения y.Таким образом, мы можем найти значения x и y, используя заданные коэффициенты и формулы.< >b=2;text< >c=-1).
Проведем расчеты для определения координат вершины.
Давайте вспомним следующее: все параболы с одинаковым коэффициентом при переменной степени имеют одинаковый внешний вид.
Значит, если мы построим параболу ( y=frac >Если мы перенесем данную функцию, так чтобы ее вершина находилась в точке (-2; -3), то получим искомый график.
Каким образом можно научиться проводить параболические кривые с высокой скоростью?
Как быстро рисовать график квадратичной функции — параболу?
Если мы пытаемся нарисовать параболу с вершиной, расположенной в начале координат, то приходится тратить много времени и неудобно строить ее точка за точкой. Однако все параболы имеют одинаковый вид, возможно, есть способ ускорить процесс их рисования?
Во время моего обучения в школе математическая учительница предложила всем изготовить трафарет из картона в форме параболы, чтобы быстро рисовать ее. Однако носить этот трафарет с собой повсюду не получится, а на экзамене его использование запрещено. Следовательно, мы не будем прибегать к использованию внешних предметов и будем искать закономерность.
Рассмотрим простейшую параболу ( y= >Построение ее может осуществляться на основе 7 точек.
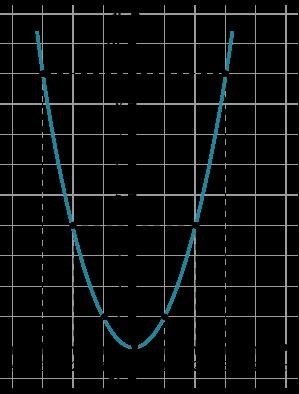
В данном случае наблюдается определенный закон.
Если сместиться вправо на 1 и вверх на 1 от вершины, то достигнем точки, принадлежащей параболе.
Далее: при перемещении из данной точки вправо на 1 и вверх на 3 мы снова вернемся в точку, принадлежащую параболе.
После этого: двигаемся вправо на (displaystyle 1) и вверх на (displaystyle 5). Что делаем дальше?
Вправо на (frac{1}{7}) и вверх на (frac{7}{49}).
Итак, продолжим движение: происходим вправо на (displaystyle 1), а затем поднимаемся вверх на следующее нечетное число.
Подобно этому поступим и с левой ветвью (ведь пара бола симметрична, следовательно, ветви выглядят одинаково).
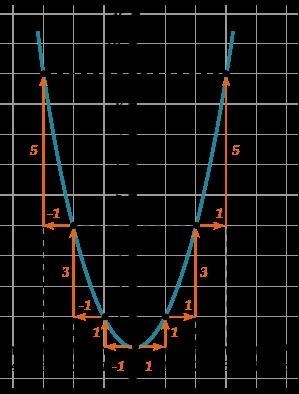
Отлично, при помощи этого метода можно построить параболу с любым значениям старшего коэффициента, равным 1.
Конструкция параболы в сжатые сроки
Известно, что вершина параболы находится в координатах (1, -2). Прошу вас нарисовать эту параболу самостоятельно на бумаге.
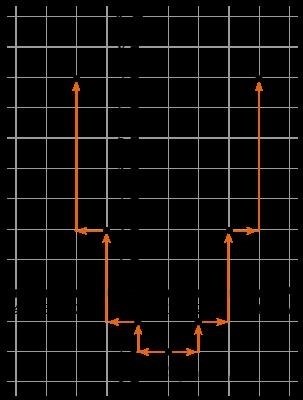
Теперь объединяем эти точки вместе:
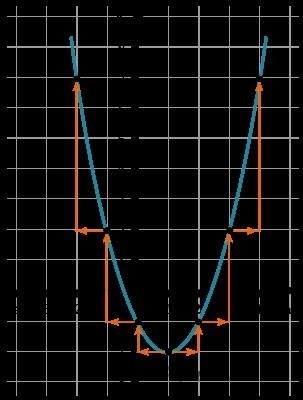
Хорошо, теперь мы будем строить только параболы с коэффициентом (displaystyle a=1)
Однозначно, нет. В данный момент мы рассмотрим, как поступить с ними, если а не равно 1.
Три типичных случая построения параболы
Ситуация 1. (когда a равно минус один).
То есть функция выглядит как ( y=- >Не так уж это и сложно. Просто опрокинем параболу рогами вниз и двигайтесь в этом направлении.
Аналогичное действие, но в направлении налево.
Случай 2. ( a>1).
Если, к примеру, задано условие ( a=2), то как быть?
Все элементарно: стартуем аналогично: ( 1) вправо, но при достижении направления «вверх» увеличиваем любую цифру в ( 2) раза.
В общей ситуации это выглядит так:
То же самое правило применяется: любое движение вправо или влево сопровождается движением вверх или вниз на определенное нечетное число, умноженное на а.
Однако всегда лень измерять нецелые (дробные) отрезки. Поэтому иногда удобнее поступить иначе: вместо шага вправо или влево на (1), сделать шаг на (frac{1}{2}).
Например: построим график ( y=-frac >Давайте будем приберегать:
Хорошо, мы успешно освоили рисование параболы, теперь давайте попрактикуемся на реальных функциях.
Как построить график квадратичной функции
Как построить график квадратичной функции
Для многих учащихся строить график квадратичной функции всегда было вызовом. Основная причина заключается в недостаточном объеме времени, уделенном этой важной теме на уроках в школе. В результате, когда возникает необходимость, ученику крайне сложно найти четкий алгоритм построения графика квадратичной функции (параболы) в школьном учебнике или в интернете, приходится тщательно искать нужную информацию по крупицам из различных источников. Но теперь мы решаем эту проблему однажды и навсегда! В данной статье опытным репетитором по математике и физике представлен алгоритм, который поможет вам построить параболу.
Алгоритм построения графика функции y=ax²+bx+c
Рассмотрим задачу построения графика квадратичной функции на конкретном примере. Пусть у нас есть функция вида: , где и .
1. Определим, куда направлены ветви соответствующей параболы. Если 0″ width=»47″ height=»14″ />Если коэффициент a в уравнении параболы положительный, то ее ветви направлены вверх, а если коэффициент a отрицательный, то ветви параболы направлены вниз.
В данном примере мы имеем дело с ситуацией, в результате чего ветви параболы ориентированы вниз.
Для определения координат вершины параболы необходимо использовать формулу для вычисления абсциссы вершины параболы.
Найти значение ординаты вершины параболы можно, подставив в уравнение квадратичной функции и вычислив соответствующее значение.
В данном экземпляре значение абсциссы вершины параболы равно:
Таким образом, значение ординаты вершины параболы определается следующим образом:
3. Давайте определим несколько дополнительных точек, находящихся неподалеку от вершины и принадлежащих параболе. Чтобы визуально представить эти точки, мы можем представить их в виде таблицы.
В данной ситуации мы получаем следующий набор данных:
| -2 | -1 | 0 | 1 | 2 | 3 | |
| -8 | 0 | 4 | 4 | 0 | -8 |
После установки точек и вершины параболы на плоскости координат, их необходимо соединить кривой линией, чтобы получить график квадратичной функции.
В данной ситуации формируется следующая кривая в форме параболы: